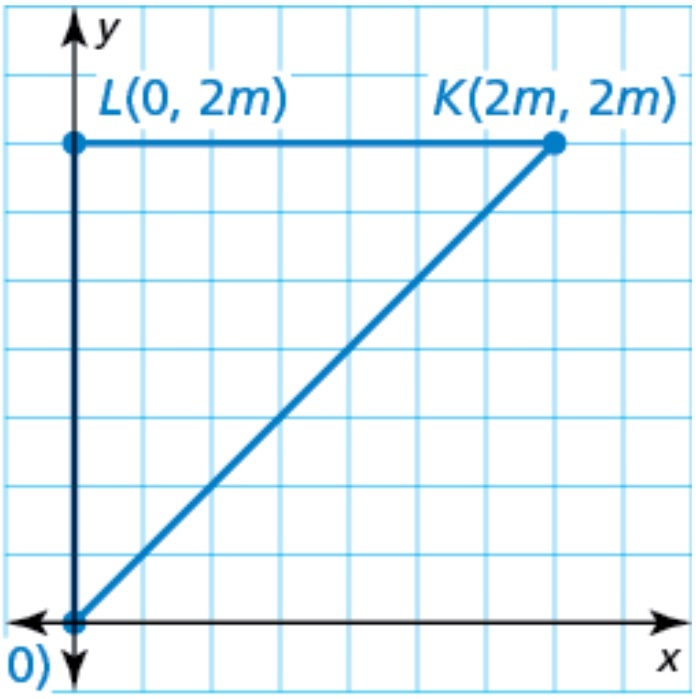
5.8 Coordinate Proofs
Assessment
•
Anne Madridano
•
Mathematics
•
9th - 11th Grade
•
120 plays
•
Hard
+10
Student preview

10 questions
Show all answers
1.
MULTIPLE CHOICE
45 sec • 1 pt
1. How is a coordinate proof different from other types of proofs you have studied?
Tags
2.
MULTIPLE CHOICE
45 sec • 1 pt

2. Explain why it is convenient to place a right triangle on the grid as shown when writing a coordinate proof.
Tags
3.
MULTIPLE CHOICE
45 sec • 1 pt
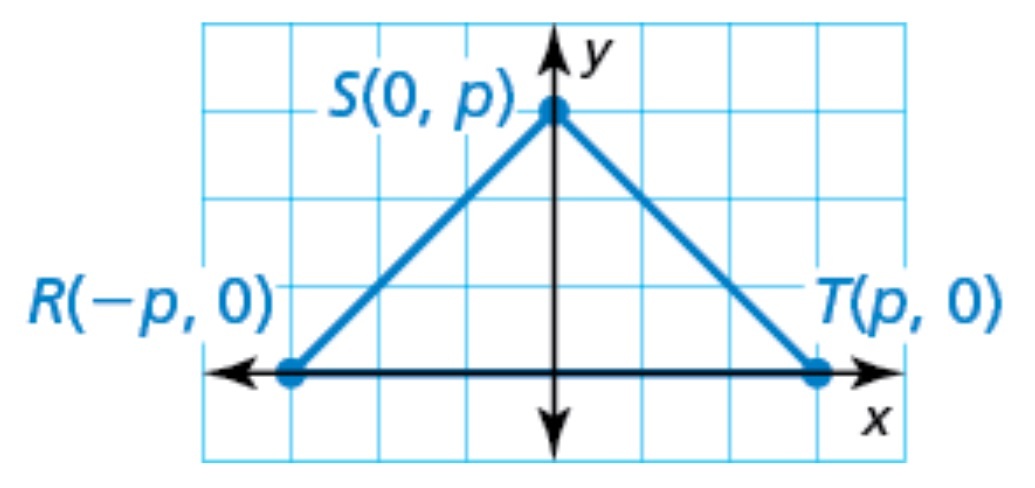
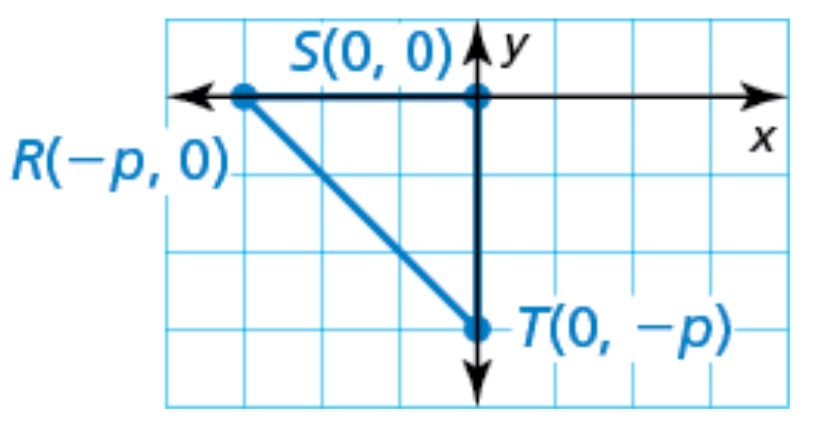
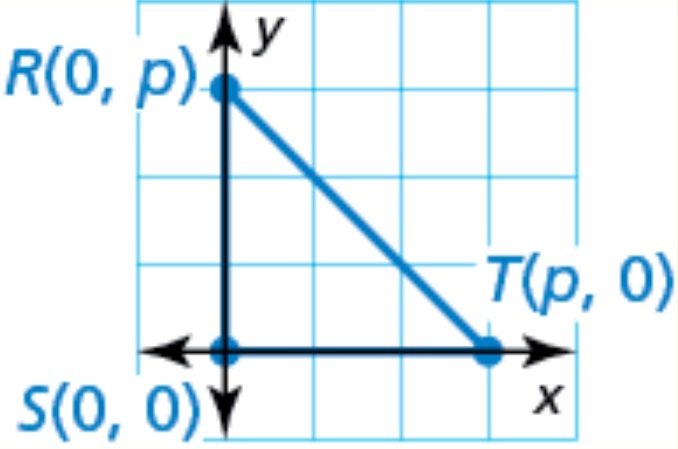
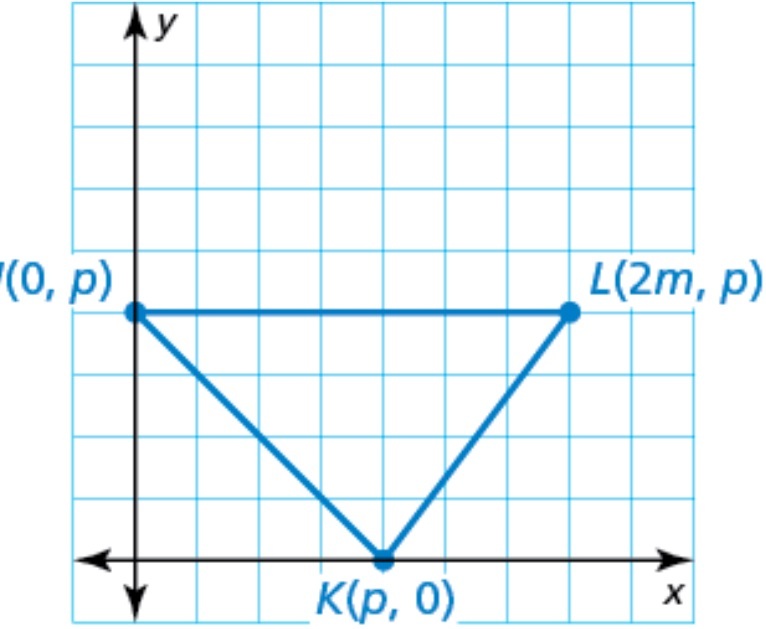
Select the graph that represents an isosceles right triangle with leg length p in the most convenient way.
Tags
4.
MULTIPLE CHOICE
45 sec • 1 pt
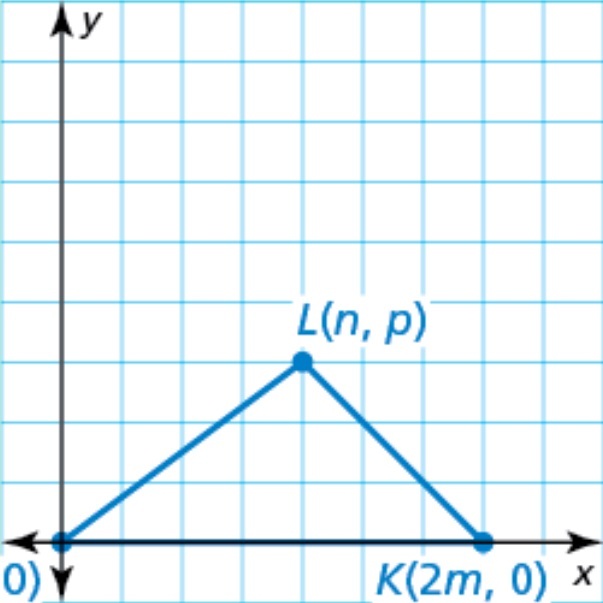
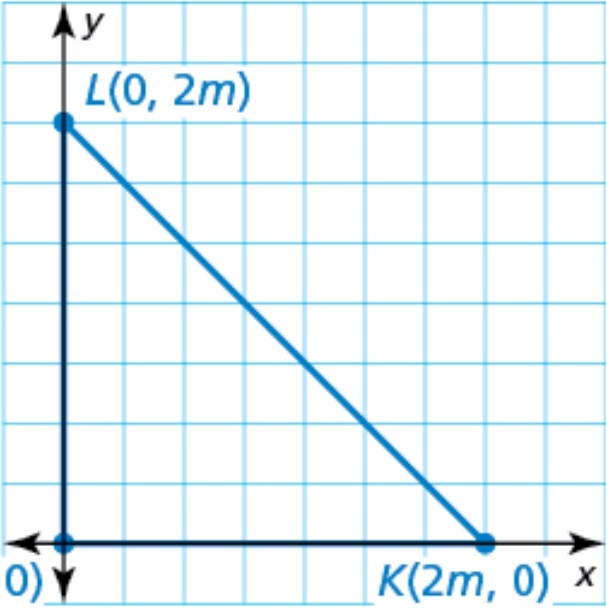
Select the most convenient graph to represent a scalene triangle with one side length of 2m.
Tags
5.
MULTIPLE CHOICE
2 mins • 1 pt

Write a plan for the proof.
Given Coordinates of vertices of △OPM and △ONM
Prove △OPM and △ONM are isosceles triangles
Tags
6.
MULTIPLE SELECT
3 mins • 1 pt

Write a plan for the proof.
Given: G is the midpoint of HF
Prove: △GHJ≅△GFO
Tags
7.
FILL IN THE BLANK
30 sec • 1 pt

Find the coordinates of the vertex O.
Tags
8.
MULTIPLE CHOICE
45 sec • 1 pt

Find the coordinates of the vertex U.
Tags
9.
MULTIPLE CHOICE
15 mins • 1 pt

You and your cousin are camping in the woods. You hike to a point that is 500 meters east and 1200 meters north of the campsite. Your cousin hikes to a point that is 1000 meters east of the campsite.
The distance from the campsite to you is ______ meters.
Tags
10.
MULTIPLE CHOICE
15 mins • 1 pt

You and your cousin are camping in the woods. You hike to a point that is 500 meters east and 1200 meters north of the campsite. Your cousin hikes to a point that is 1000 meters east of the campsite.
The distance from you to your cousin is ______ meters.
Tags
Explore all questions with a free account
Similar Resources on Quizizz

Coordinate Triangle Proofs
•
9th - 11th Grade

Coordinate Proof Geometry
•
9th - 11th Grade

Coordinate Proofs
•
10th Grade - University

Distance Formula Coordinate Grid
•
9th Grade - University

Proof on the Coordinate Grid
•
9th Grade

Coordinate Proofs
•
9th - 11th Grade

Right Triangles in Coordinate Plane
•
9th - 11th Grade

Coordinate Geometry Proofs
•
9th - 11th Grade
Popular Resources on Quizizz

STAAR reading review
•
4th - 5th Grade

7th STAAR Reading Review
•
7th Grade

STAAR Reading Review
•
4th - 7th Grade

STAAR reading vocabulary
•
4th - 5th Grade

STAAR Reading Review
•
3rd - 5th Grade

Reading STAAR Review
•
4th Grade

7th grade STAAR Reading Review
•
7th Grade

Revising and Editing
•
4th Grade
Discover more resources for Mathematics

Converting from Standard Form to Vertex Form
•
11th - 12th Grade

Discriminant
•
11th Grade

Pythagorean Theorem Basics
•
9th - 12th Grade

ACT Math Practice
•
9th - 12th Grade

Algebra 1 EOC Review 1
•
9th Grade

Special Right Triangles
•
8th - 10th Grade

Circle Equations
•
10th - 11th Grade

Graphing Quadratics: Intercepts, Vertex, and Axis of Symmetry
•
8th - 10th Grade