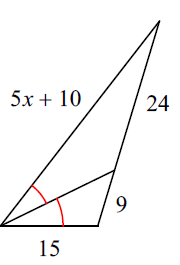Triangle Similarity Theorems

1.

Multiple Choice

30 sec

5 pts

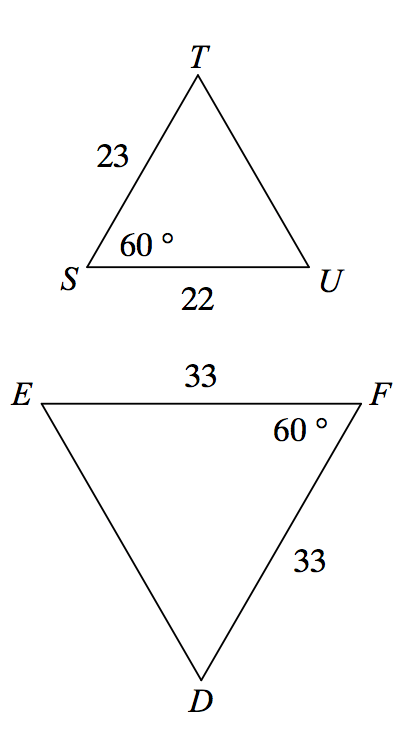
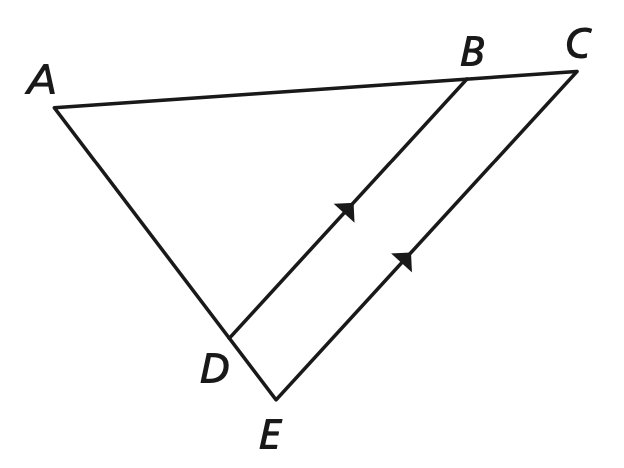
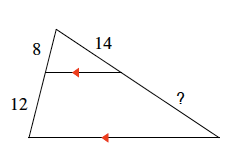
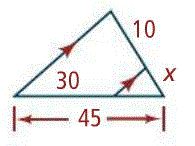
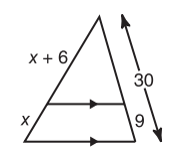
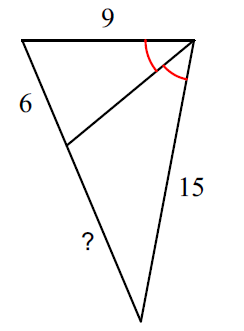
State if the triangles in each pair are similar. If so, state how you know they are similar.

Yes, AA Similarity

Yes, SSS Similarity

Yes, SAS Similarity

Not Similar

2.

Multiple Choice

30 sec

1 pt

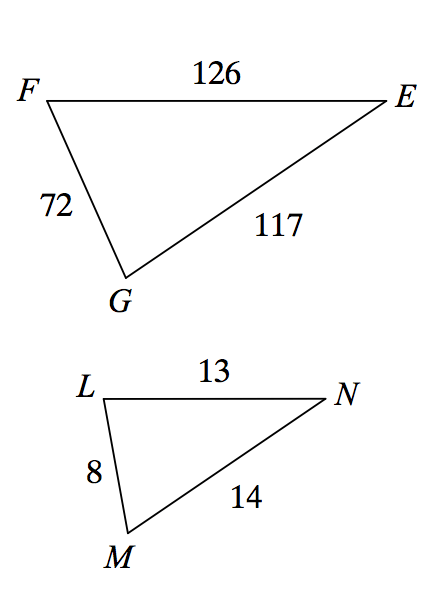
State if the triangles in each pair are similar. If so, state how you know they are similar.

Yes, AA Similarity

Yes, SSS Similarity

Yes, SAS Similarity

Not Similar

3.

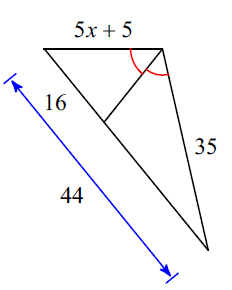
Multiple Choice

30 sec

1 pt

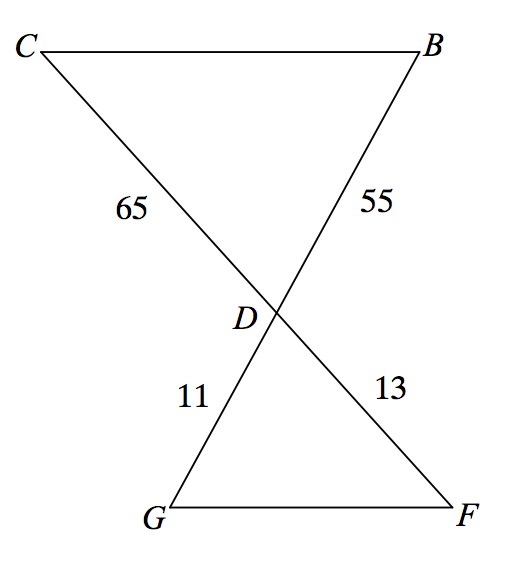
State if the triangles in each pair are similar. If so, state how you know they are similar.

Yes, AA Similarity

Yes, SSS Similarity

Yes, SAS Similarity

Not Similar

4.

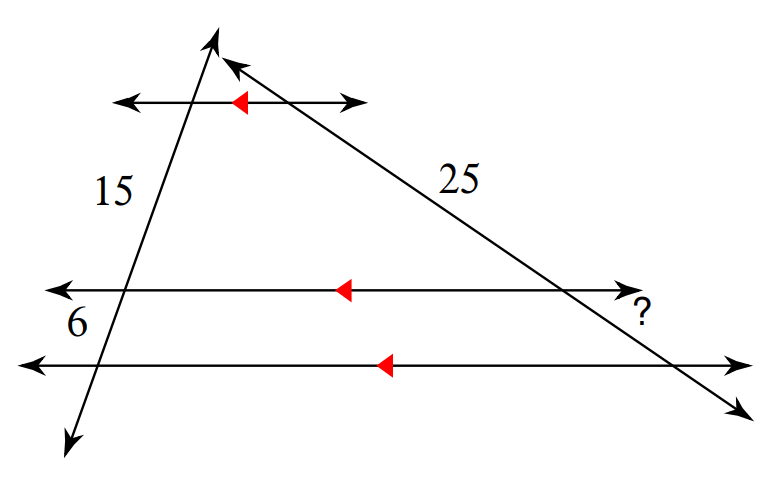
Multiple Choice

30 sec

1 pt

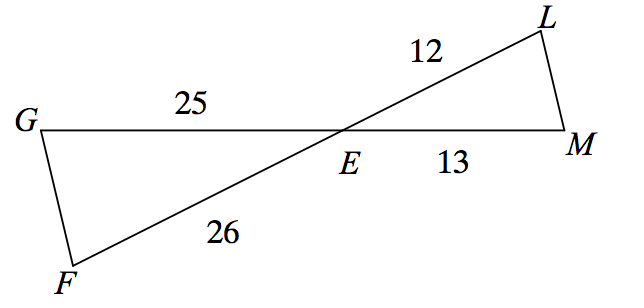
State if the triangles in each pair are similar. If so, state how you know they are similar.

Yes, AA Similarity

Yes, SSS Similarity

Yes, SAS Similarity

Not Similar

5.

Multiple Choice

30 sec

1 pt

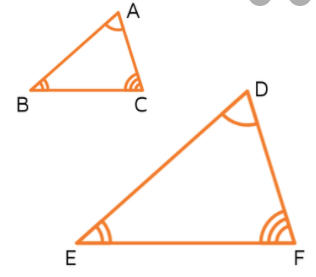
Pick the correct Similarity Statement for the Triangles shown.

ΔCAB ~ ΔDEF

ΔABC ~ ΔDFE

ΔABC ~ ΔDEF

ΔBCA ~ ΔDEF

6.

Multiple Choice

30 sec

1 pt

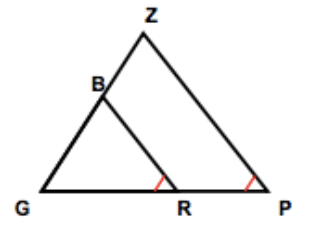
Are these two triangles similar? Which similarity criterion do you use to prove it?

Yes, AA

Yes, SAS

Yes, SSS

Not Similar

7.

Multiple Choice

30 sec

1 pt

If two figures are similar, the corresponding sides are ______________.

equal

congruent

proportional

none of these

8.

Multiple Choice

30 sec

1 pt

Complete the similarity statement: △ADB ~ _______

△ACE

△AEC

△EAC

△ECA

9.

Multiple Choice

30 sec

1 pt

The Angle-Angle Similarity (AA ~) Theorem states if two angles of one triangle are _______________ to two angles of another triangle, then the triangles are ____________________.

adjacent; equal

complementary; scalene

congruent; similar

supplementary; isosceles

10.

Multiple Choice

30 sec

1 pt

The Side-Side-Side Similarity (SSS ~) Theorem states if the corresponding sides of two triangles are _____________________, then the triangles are _________________.

proportional; similar

similar, proportional

congruent; congruent

equal; equilateral

11.

Multiple Choice

30 sec

1 pt

The Side-Angle-Side Similarity (SAS ~) Theorem states that if two sides of one triangle are ________________ to two sides of another triangle and their _________________ angles are congruent, then the triangles are similar.

adjacent; intersect

complementary; form

adjacent; create

proportional; included

12.

Multiple Choice

30 sec

1 pt

Which is not a similar triangle theorem?

ASA∼

SAS∼

SSS∼

AA∼

13.

Multiple Choice

2 mins

1 pt

Which is not a similar triangle theorem?

ASA∼

SAS∼

SSS∼

AA∼

14.

Multiple Choice

15 mins

1 pt

Find the missing length.

21

18

16

24

15.

Multiple Choice

15 mins

1 pt

Which proportion would be correct in order to solve for x.

x/10 = 15/30

x/10 = 45/30

x/10 = 15/45

x/10 = 30/15

16.

Multiple Select

45 sec

1 pt

Select ANY correct proportion that can be used to solve for x.

17.

Multiple Choice

30 sec

1 pt

According to the Triangle Angle Bisector Theorem, which proportion is set up correctly?

All of the above

18.

Multiple Select

45 sec

1 pt

Select the correct proportions to solve for x (there are multiple correct answers):

19.

Multiple Choice

30 sec

1 pt

Which is the correct proportion for solving for x?

20.

Multiple Choice

30 sec

1 pt

Write a proportion to find the length of "?"

Explore this activity with a free account