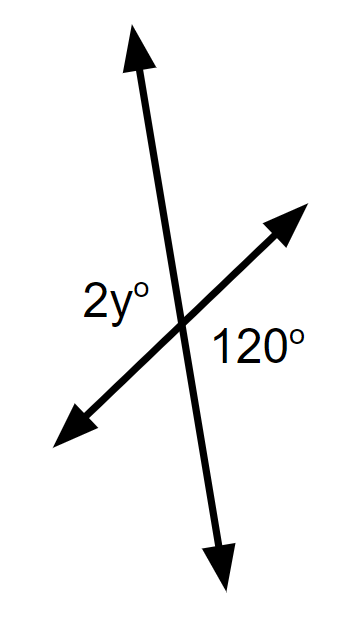
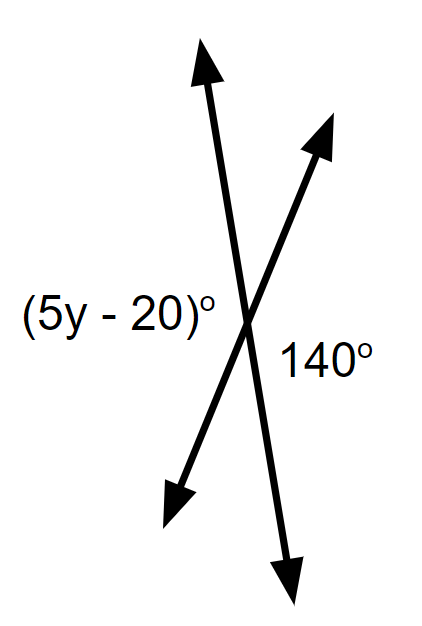
Solving Vertical Angles with 1 and 2 step equations
Assessment
•
Brian Lemoi
•
Mathematics
•
7th Grade
•
13 plays
•
Medium
Improve your activity
Higher order questions
Match
•
Reorder
•
Categorization
.svg)
actions
Add similar questions
Add answer explanations
Translate quiz
Tag questions with standards
More options
10 questions
Show answers
1.
Multiple Choice
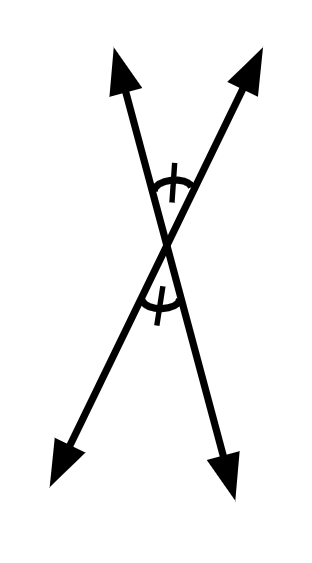
These two lines intersect and create 4 angles. The angles that are opposite of each other are called what?
Vertical Angles
Criss-Cross angles
X-Men Angles
Parallel Angles
2.
Multiple Choice
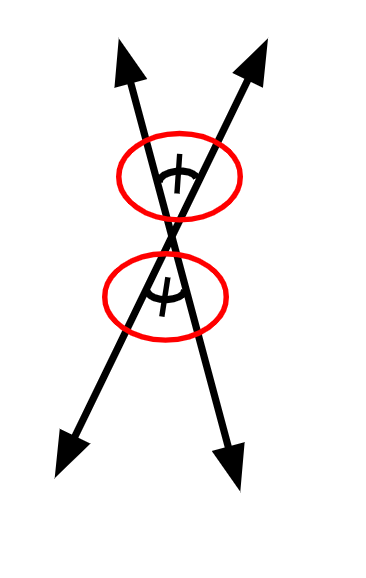
Those things in the red circles are called hatch marks. Both of these angles have 1 hatch mark. That means they are EQUAL TO EACH OTHER. When an angle has the same number of hatch marks as another angle, they are equal to each other.
Based on this, what can we conclude about Vertical Angles?
They are EQUAL TO EACH OTHER.
They are equal to 180 degrees
They are equal to 90 degrees
They are equal to 360 degrees
3.
Multiple Choice
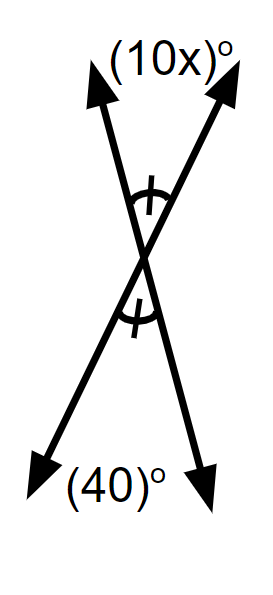
These angles are vertical angles. One is 40 degrees, the other is 10x degrees. What equation can we use to find the value of x?
10x + 40 = 180
10x = 40
10x + 40 = 90
10x + 40 = 100
4.
Multiple Choice
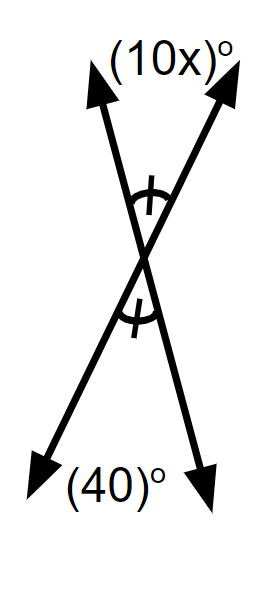
These are vertical angles so we know they are EQUAL TO EACH OTHER. So we can use the formula:
10x = 40
Solve for x.
x = 10
x = 40
x = 4
x = 30
5.
Multiple Choice
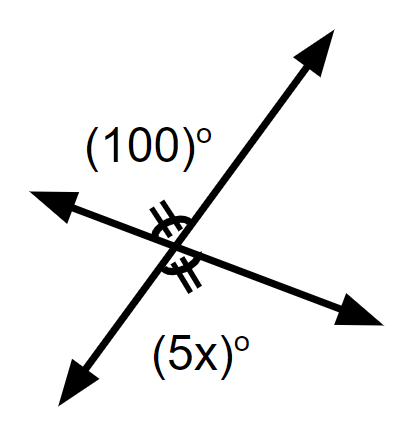
These are vertical angles. One is 100 degrees the other is 5x degrees. What equation would we use to solve for x?
5x + 100 = 180
5x + 100 = 90
5x = 100
5x - 100 = 80
6.
Multiple Choice

These are vertical angles. One is 100 degrees the other is 5x degrees.
We can use the equation 5x = 100
Solve for x
x = 80
x = 20
x = 120
x = 40

Explore this activity with a free account
Find a similar activity
Create activity tailored to your needs using
.svg)

Missing Angles in Triangles
•
6th Grade

Measuring Angles
•
4th - 5th Grade

Parallel Lines
•
9th Grade

Parallel Lines & Transversals
•
9th - 10th Grade

Angle Relationships
•
8th Grade

Angles and Angle Relationships
•
8th Grade

Corresponding Angles
•
10th Grade

Parallel Lines & Transversals
•
10th - 11th Grade