Chapter 2 Test Review

1.

Multiple Choice

2 mins

1 pt

Page 137 #T.2.1 (Interpreting Percentiles)

a

b

c

d

e

Answer explanation

The percentile tells you the percent of the data set that is at or below a specific piece of data.

2.

Multiple Choice

2 mins

1 pt

Page 138 #T.2.5 (Calculate the standard deviation from a percentile.)

a

b

c

d

e

Answer explanation

15% is the area to the right of 60 inches. You need to look in Table A for 0.85, which is the area to the left. Then use the corresponding z-score and the z-score formula to solve for the standard deviation.

3.

Multiple Choice

2 mins

1 pt

Page 138 #T.2.7 (Calculate the standard deviation using the empirical rule)

a

b

c

d

e

Answer explanation

Using the 68-95-99.7 rule, if 99.7% of the data lies between 5 ft & 7ft, these numbers are both 3 standard deviations from the mean. The mean is between them at 6ft., so the standard deviation must be 1/3 of a foot (4 inches).

4.

Multiple Choice

2 mins

1 pt

Page 138 #T.2.10 (Comparing Standardized Scores)

a

b

c

d

e

Answer explanation

Calculate the z-scores for each student. The student with the higher z-score performed better compared to their peers.

5.

Multiple Choice

2 mins

1 pt

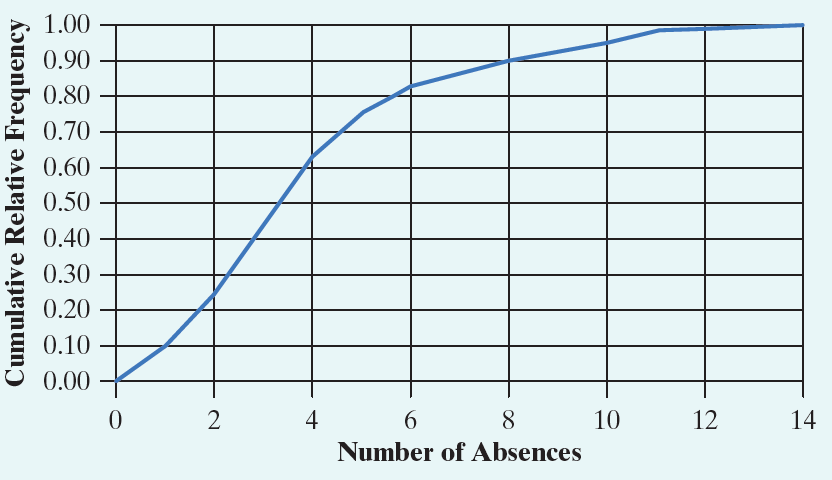
The number of absences during fall semester was recorded for each student in a large elementary school. The distribution of absences is displayed in the following cumulative relative frequency graph. What is the IQR for the distribution of absences?

1

2

3

5

1

Answer explanation

Q1 is found at the 25th percentile. Q3 is found at the 75th percentile. Subtract those values to find your IQR.

6.

Multiple Choice

2 mins

1 pt

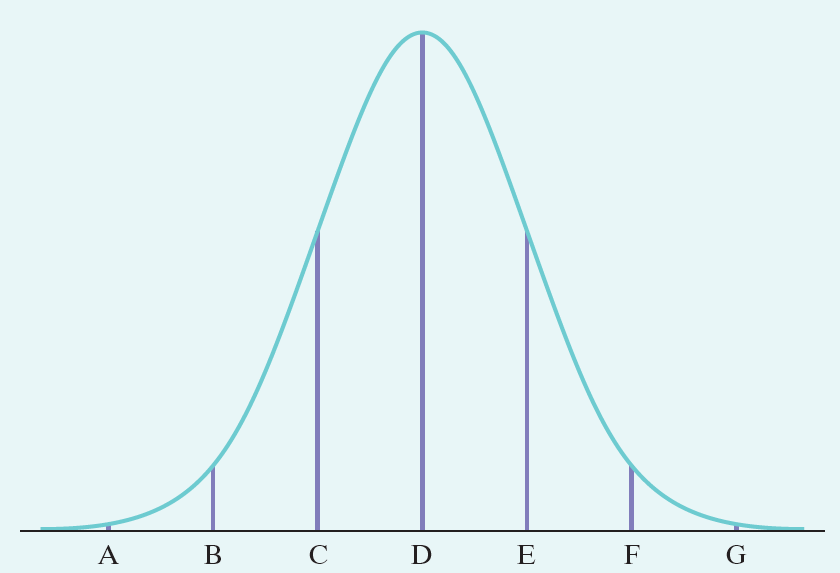
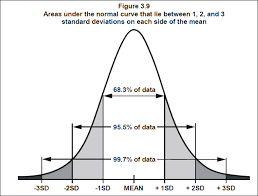
The weights of laboratory cockroaches follow a Normal distribution with mean 80 grams and standard deviation 2 grams. The following figure is the Normal curve for the distribution of weights. About what percent of the cockroaches have weights between 76 and 84 grams?

99.7%

95%

68%

47.5%

34%

Answer explanation

Use the empirical Rule (68-95-99.7 rule). Since 76 & 84 are both 2 standard deviation from the mean, this rule is easily applied.

7.

Multiple Choice

2 mins

1 pt

For the density curve shown, which of the following statements is true?

The mean is larger than the median.

The proportion of outcomes between 0.2 and 0.5 is equal to 0.3.

The proportion of outcomes greater than 1.5 is equal to 0.25.

The area under the curve is 2.

Answer explanation

This is a uniform distribution. The area of the curve is length times width.

8.

Multiple Choice

2 mins

1 pt

The cumulative relative frequency graph describes the distribution of weights (in grams) of tomatoes grown in a laboratory experiment. Which of the following weights is closest to the median of the distribution?

120 grams

140 grams

170 grams

200 grams

Answer explanation

The median is found at the 50the percentile.

9.

Open Ended

15 mins

1 pt

Page 139 #T.2.12 (Percentile, finding percentage, finding the IQR)

Evaluate responses using AI:

OFF

Answer explanation

a) 23.9 is 1 standard deviation above the mean. Use the 68-95-99.7 rule to determine the are under the curve.

b) Find z-scores for 20 inches & 26 inches. Then use table A to find the area between those z-scores.

c) Q1 will be found at 25% and Q3 will be found at 75%. Use these values on Table A to come up with the z-scores for those data points.

10.

Open Ended

15 mins

1 pt

Page 139 #T.2.13 (Assessing Normality)

Evaluate responses using AI:

OFF

Answer explanation

The mean & median are not close to each other.

The distance between the median and the minimum is very different than the distance from the median to the maximum. If the distribution was Normal, these would be much more similar because of the symmetric nature.

11.

Open Ended

15 mins

1 pt

Page 136 #R.2.2 (Reading a Cumulative Relative Frequency Graph)

Evaluate responses using AI:

OFF

Answer explanation

a) follow the graph from 7 hours on the x-axis to the curve and over to the y-axis to determine the percentiles.

b) find 25% on the y-axis, follow that to the curve & down to the x-axis. This is Q1. Do the same thing with 75% to find Q3.

12.

Open Ended

15 mins

1 pt

Page 136 #R.2.5 (Empirical Rule & Using Table A)

Evaluate responses using AI:

OFF

Answer explanation

a) Use the empirical rule (68-95-99.7 rule) to determine the limits 3 standard deviations from the mean.

b) Calculate the z-score of 339. Then use table A to find the percent.

13.

Open Ended

15 mins

1 pt

Page 137 #R.2.7 (Using Table A & Finding Quartiles)

Evaluate responses using AI:

OFF

Answer explanation

a) Calculate the z-score, then use table A to find the percent.

b) Find 25% and 75% in table A. Then use the corresponding z-score to find the weights.

14.

Multiple Choice

30 sec

1 pt

Jorge's score on Exam 1 in his statistics class was at the 64th percentile of the scores for all students. His score falls

between the minimum and first quartile

between the first quartile and the median

between the median and the third quartile

between the third quartile and the maximum

at the mean score for all students

Explore this activity with a free account