Centers of Triangles
Assessment
•
Kristen Barclay
•
Mathematics
•
9th - 10th Grade
•
839 plays
•
Medium
Improve your activity
Higher order questions
Match
•
Reorder
•
Categorization
.svg)
actions
Add similar questions
Add answer explanations
Translate quiz
Tag questions with standards
More options
22 questions
Show answers
1.
Multiple Choice
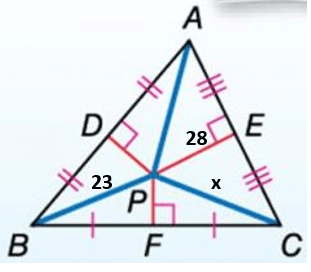
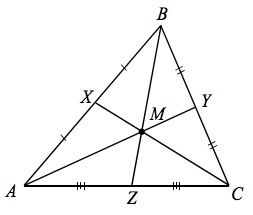
The centroid is the 3 ____ of a triangle intersect.
Medians
Midsegments
Perpendicular Bisectors
Angle Bisectos
2.
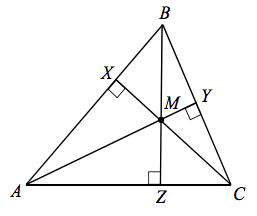
Multiple Choice
The point where the 3 perpendicular bisectors of a triangle cross is called the ___?
Midsegment
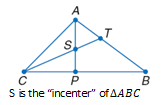
Incenter
Circumcenter
Centroid
3.
Multiple Choice

angle bisector
perpendicular bisector
median
midsegment
4.
Multiple Choice
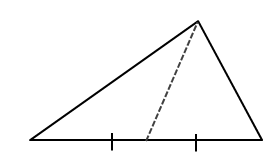
angle bisector
midsegment
altitude
median
5.
Multiple Choice
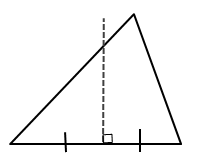
altitude
perpendicular bisector
midsegment
angle bisector
6.
Multiple Choice
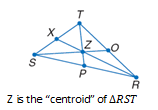
angle bisectors
perpendicular bisectors
altitudes
medians

Explore this activity with a free account
Find a similar activity
Create activity tailored to your needs using
.svg)

Classifying Triangles
•
6th - 8th Grade

Classifying Triangles
•
4th - 5th Grade

Classifying Triangles
•
4th Grade

Special Right Triangles
•
10th Grade

Pythagorean Theorem
•
9th Grade

Pythagorean Theorem
•
8th Grade

Pythagorean Theorem
•
9th Grade

Pythagorean Theorem
•
8th Grade