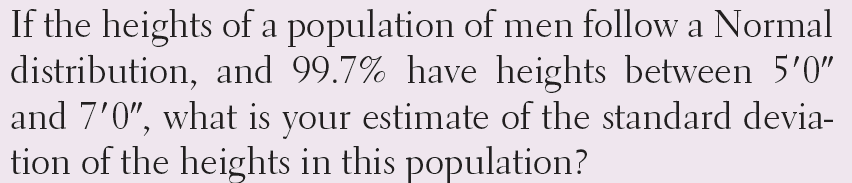AP Stats: Chapter 2 Multiple Choice Practice Test
Assessment
•
CHRISTOPHER IRELAND
•
Mathematics
•
11th - 12th Grade
•
856 plays
•
Medium
Improve your activity
Higher order questions
Match
•
Reorder
•
Categorization
.svg)
actions
Add similar questions
Add answer explanations
Translate quiz
Tag questions with standards
More options
20 questions
Show answers
1.
Multiple Choice

Pete's score was below the median.
Pete did worse than about 63% of the test takers.
Pete did worse than about 73% of the test takers.
Pete did better than about 63% of the test takers.
Pete did better than about 73% of the test takers.
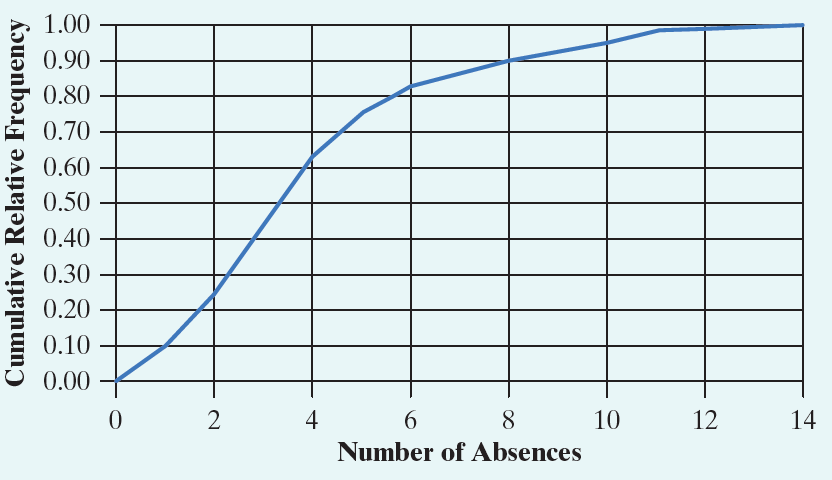
2.
Multiple Choice
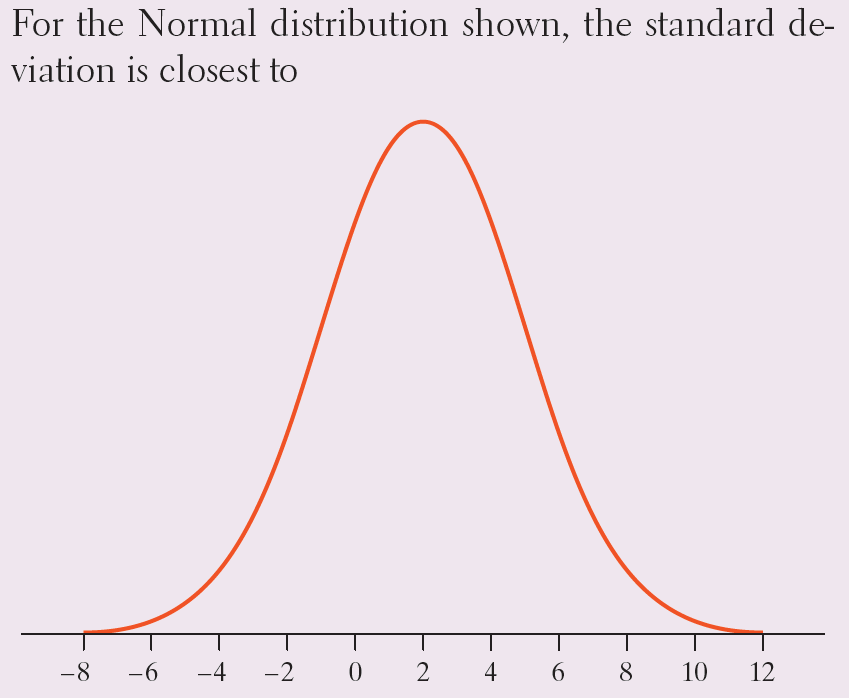
0
1
2
3
5
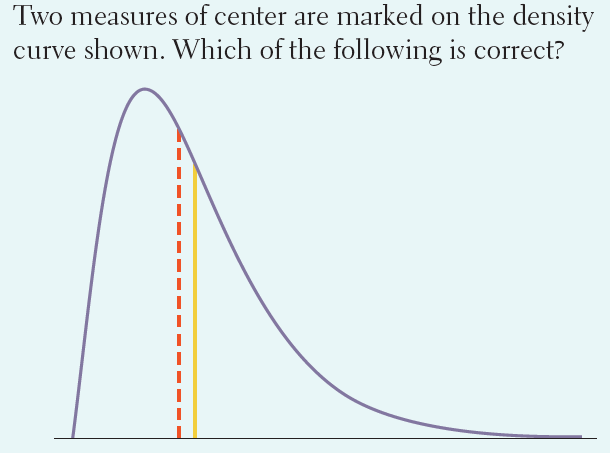
3.
Multiple Choice

5.64, 1.44
5.64, 1.32
5.40, 1.44
5.40, 1.32
5.64, 1.20
4.
Multiple Choice
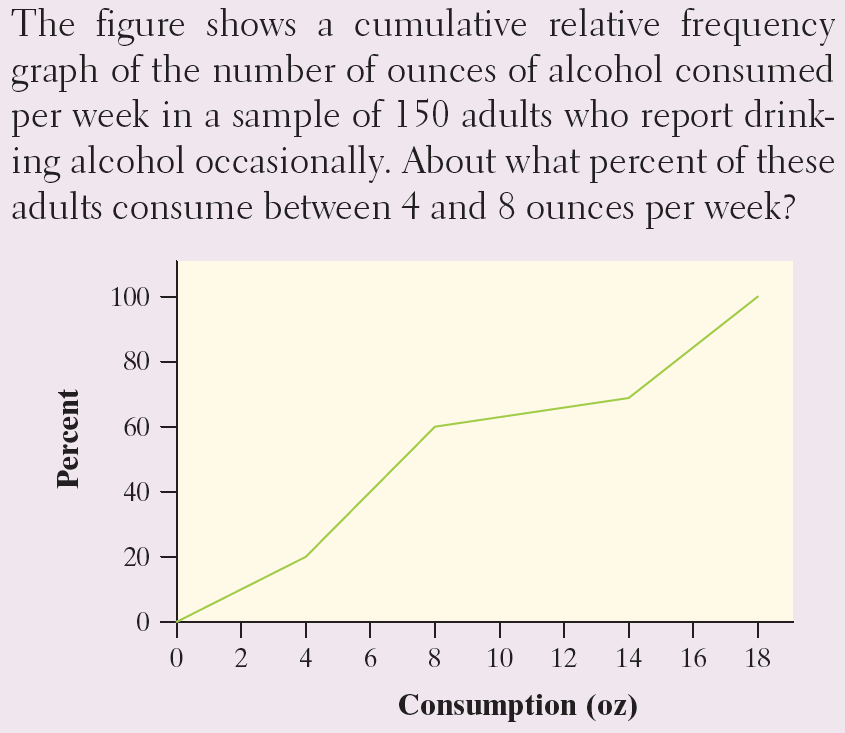
20%
40%
50%
60%
80%
5.
Multiple Choice

4.83 inches
5.18 inches
6.04 inches
8.93 inches
The standard deviation cannot be computed from the given information.
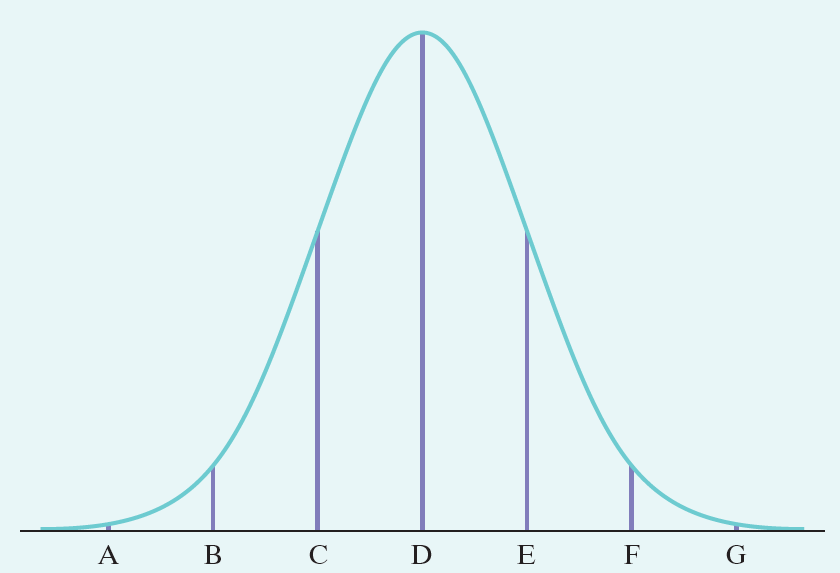
6.
Multiple Choice
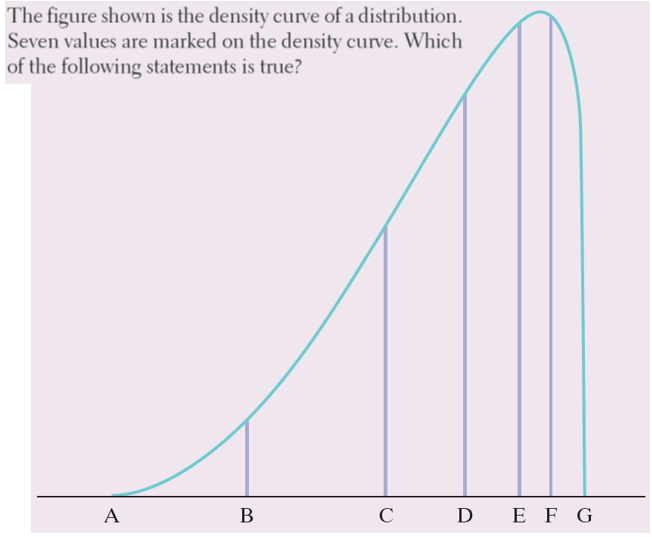
The mean of the distribution is E.
The area between B and F is .50.
The median of the distribution is C.
The 3rd quartile of the distribution is D
The area under the curve between A and G is 1.

Explore this activity with a free account
Find a similar activity
Create activity tailored to your needs using
.svg)

Arsenal Quiz
•
KG

Measures of Spread
•
KG

Scatter Plots
•
KG

Numeros
•
KG

Prepositions
•
KG

Tens and Ones
•
KG

Adding with Pictures
•
KG

Kindergarten Math
•
KG